جواب سوال سر کلاس موازی
In unweighted bipartite graphs[edit]
Matching problems are often concerned with bipartite graphs. Finding a maximum bipartite matching[3] (often called a maximum cardinality bipartite matching) in a bipartite graph
is perhaps the simplest problem.
The Augmenting path algorithm finds it by finding an augmenting path from each x ∈ X to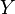 
and adding it to the matching if it exists. As each path can be found in 
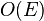time, the running time is 
. This solution is equivalent to adding a super source 
with edges to all vertices in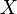 
, and a super sink 
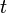with edges from all vertices in 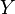, and finding amaximal flow from 
to 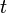. All edges with flow from 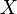to 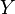then constitute a maximum matching.
An improvement over this is the Hopcroft–Karp algorithm, which runs in 
time. Another approach is based on the fast matrix multiplication algorithm and gives 
complexity,[4] which is better in theory for sufficiently dense graphs, but in practice the algorithm is slower.[5]
