Feedback vertex set

http://www.cs.cmu.edu/afs/cs/academic/class/15854-f05/www/scribe/lec9.pdf

http://www.sciencedirect.com/science/article/pii/S0022000008000500

جواب سوال سر کلاس موازی

صورت سوال را قبلاً گذاشتم اما تا الآن وقت نکرده بودم جوابش را بگذارم: (منبع ویکیپدیا)

In unweighted bipartite graphs[edit]

Matching problems are often concerned with bipartite graphs. Finding a maximum bipartite matching^[3] (often called a maximum cardinality bipartite matching) in a bipartite graph is perhaps the simplest problem.

The Augmenting path algorithm finds it by finding an augmenting path from each x ∈ X to 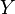 and adding it to the matching if it exists. As each path can be found in  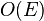time, the running time is . This solution is equivalent to adding a super source  with edges to all vertices in 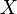, and a super sink  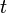with edges from all vertices in 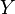, and finding amaximal flow from  to 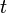. All edges with flow from  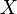to 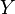 then constitute a maximum matching.

An improvement over this is the Hopcroft–Karp algorithm, which runs in  time. Another approach is based on the fast matrix multiplication algorithm and gives  complexity,^[4] which is better in theory for sufficiently dense graphs, but in practice the algorithm is slower.^[5]

بیان!

الآن بیان فکر کرده من میرم پول میدم که همین وبلاگ را ادامه بدهم؟ عمراً.

اگر ظرفیتش تموم بشه (که انگار این داره تموم میشه، مثلاً موضوعاتش رو دیگه نمیشه اضافه کرد)‌ یکی دیگه می‌زنم.

گفتم در جریان باشید!

بدون شرح!

http://www.informatik.uni-trier.de/~ley/pers/hd/a/Abam:Mohammad_Ali

cake cutting

http://iiis.tsinghua.edu.cn/~eccs/eczb6.pptx

Balanced Graph Partitioning

http://www.dcs.warwick.ac.uk/~harry/pdf/bpartition.pdf

A Course in Data Intensive Computing

http://www.sics.se/~amir/dic.htm

شبکه‌های جهان کوچک

این مطلب درخواستی یکی از دوستان است! :) برای اینکه مطلب مفهوم‌تر باشد سعی کردم از یک منبع کمک بگیرم!

مرجع: http://www.cs.cornell.edu/home/kleinber/networks-book/networks-book-ch20.pdf

۱- درجه جدایی ۶:

یعنی در گراف آن با طی کردن ۶ یال از هر رأسی می‌توانیم به هر رأس دیگری برسیم.

داستان آن از اینجا شروع شده است که یک نفر یک سری نامه برای چند نفر فرستاده و خواسته که آنها برای یک آدم خاص بفرستند یا به کسی بفرستند که آن فرد را می‌شناسد. و به طور میانگین (expected) با ۶ گام نامه‌ها به مقصد رسیده‌اند.

۲- ساختار و تصادفی بودن:

گفتیم به صورت متوسط این اتفاق می‌افتد. این کار را با محاسبه امیدریاضی انجام می‌دهند. می‌شود ساختارهایی ساخت که این خاصیت را دارند، اما سوال اصلی این است که گرافی مثل شبکه‌ی اجتماعی چرا این خاصیت را دارد؟ چون مثلاً در گرافهایی که مطمئنیم این خاصیت برقرار است مثلاً در مثال زیر فرض می‌کنیم هر نفر ۳ دوست دارند که آنها هم ۳ دوست جدید دارند و ...، در حالی که در عمل این طور نیست و اکثراً بین دوست‌های افراد اشتراک هست.

برای اینکه مشکل تعداد دوست‌های جدید را حل کنیم، فرض می‌کنیم هر کسی تعداد دوست جدید کمی دارد ولی به جای آن دوست با فاصله‌ی زیاد از همسایه‌هایش به آن می‌دهیم. مثال زیر را در نظر بگیرید که در آن یک توری داریم و یک سری یال تصادفی به آن اضافه کرده‌ایم.

مدل Watts-Strogatz:

کافی است فقط تعدادی از افراد در شبکه تصادفی، لینک (یال) به یک فرد دور داشته باشند.

جستجوی غیرمتمرکز:

حالا سوال این است که از یک مبدأ به یک مقصد بدون دانستن لینک‌های تصادفی چطور باید یک بسته را بفرستیم؟

هر کسی به صورت محلی این طور عمل می‌کند که بسته را به نزدیک‌ترین همسایه‌اش به هدف می‌فرستد.

این کار در حالت عادی زمان زیادی می‌گیرد ولی اگر طول لینک‌های تصادفی از حدی بیشتر باشد این زمان کم می‌شود.

از اینجا به بعد وارد محاسبات شده است اگر خواستید خودتان بخوانید. من هم فقط سر یک talk رفتم در مورد این و چیز بیشتری نمی‌دانم و اگر بخواهم توضیح بدهم باید خودم اول بخوانم.

تمرین تقریبی ۲

http://ce.sharif.edu/courses/92-93/2/ce726-1/assignments/files/assignDir17/exercise%202.pdf

کدینگ

کدینگ در شبکه:

به جای اینکه خود اطلاعات را بفرستیم کد آنها را بفرستیم.

مثال: دو نفر می‌خواهند پیامشان را از طریق یک سرور ارسال کنند. هر دو پیام را به سرور می‌فرستند و در آنجا xor پیام محاسبه می‌شود و برای هر کس فرستاده می‌شود. با این کار هر دو پیام را با xor کردن با پیام خودشان به دست می‌آورند.

مثال: دو مبدأ می‌خواهند پیامشان را به دو مقصد بفرستند. هر کس وقتی پیام خودش را می‌فرستد، بقیه هم دریافت می‌کنند، اینجا بر خلاف قبل آن را دور نمی‌ریزند. در این صورت وقتی سرور xor پیام را می‌فرستد آنها هنوز قادرند پیام اولیه را به دست بیاورند.

در هر دو مثال بالا تعداد ارسال‌ها از ۴ گام به ۳ گام کاهش داده می‌شود.

کدینگ حافظه:

در پایگاه داده‌ها ما از افزونگی برای جلوگیری از نابودی اطلاعات به دلیل مشکل سخت‌افزاری استفاده می‌کنیم. Reed-Solomon یکی از این روش‌ها است. A+B و A+2B را به جای سه تا نمونه از هر کدام نگه می‌داشت. (اگر دو تا خراب بشه باز هم کار می‌کند.)

الگوریتم:

داده‌ها را به ۱۰ بلوک تقسیم می‌کنیم و با ۵ تا رابطه که هر کدام بر حسب ۵ تا بلوک هستند می‌توانیم جواب مسأله را حساب کنیم. اما می‌توان طوری این روابط را محاسبه کرد که تکراری داشته باشند و نیاز به ۲۵ عمل نداشته باشیم. برای ۲۰ تا رابطه‌ی آن ارائه شد. سوال: آیا کمتر هم می‌شود؟